
Tutoring and Puzzles!
or to Fred's Navigator

or to Fred's Navigator
 |
THE LITTLE TRIANGLE MOVIE | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| for Fun, Learning, Education, Tutoring and Puzzles! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FREDSHOUSE | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Go to Fred's Main Page or to Fred's Navigator |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fred's Little Triangle Movie | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Pythagorean Theorem! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Watch the little triangle movie a couple of times and then come back and we'll watch it together... | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Let's look at what happens in the movie. It starts with a blue triangle tumbling in from the right side of the screen... It ends up falling into exactly the "right" place. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The blue triangle is then exactly copied, but as a pink triangle, and together they form a rectangle. From the short side of the rectangle a black square is formed. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then two more triangles, first green then orange, both also just like the original blue triangle, appear alongside the little black square. This "accidentally" happens to form a second black square, from another side of the triangle! Now we have one large overall square divided into four colored triangles and two black squares. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now the blue triangle appears again to the right, just in the "right" place, of course. And the pink, orange and green triangles appear in just the "right" places also. The four triangles happen to surround a square, which now turns black. But they also form an outside or overall square, which is the same size as the overall square on the left side. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The squares now fade to grey in the same order as they originally appeared in the movie. They then return to the original black in the same order, first the little black square, then the middle black square, finally the large black square. That's the end of the movie. But watch it again! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| What it shows is that the area occupied by the two smaller black squares in the left-side overall square is the same area as the area occupied by the larger black square in the right-side overall square. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because the left and right overall squares are the same size, and because the same four triangles (blue, pink, orange and green) are placed inside these squares, the areas left over by the triangles are also the same! The area of square one plus the area of square two equals the area of square three. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| So The Little Triangle Movie actually proves something! It proves what is called "The Pythagorean Theorem," named after Pythagoras, the Greek mathematician and mystic who discovered it. To find out more about Pythagoras and his theorem use the links below. But remember, it is pretty certain that the theorem was discovered by others than Pythagoras and earlier than Pythagoras! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This does not work for all triangles! Only "right" triangles. A right triangle has one angle that is 90 degrees. If you were to stand up straight right now (stand "upright") the angle formed by your body and the floor would be a right or 90 degree angle. You would be "perpendicular" to the floor. Hope you have a flat floor or this would not be true! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (There are 360 degrees in a circle. Just because someone said so and because 360 = 2 X 2 X 2 X 3 X 3 X 5, which makes it divisible by a lot of convenient numbers such as 2, 3, 10 and 12. A right angle is one fourth of a circle or 90 degrees. A line going through the middle of a circle divides it in half, so a line is 180 degrees. Crossing the line straight up and down -- "making a perpendicular" -- divides the line's angle in half, forming a 90 degree, or a right, angle.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
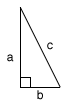
| This is what a right triangle looks like. The little box shows the right angle. a and b are the two shorter sides. They are "arms" of the right angle. c is the hypotenuse, the side opposite the right angle. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you looked at a spot on the floor a little distance from you and imagined a line going from your eyes to that spot, that line along with your body and the floor would form a triangle. This would be a "right" triangle. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The imaginary line from your eyes to the spot would be the line opposite the right angle formed by your body and the floor. This line is called by a funny name! It is called the hypotenuse of the right triangle, and is defined as the side of a right triangle that is opposite the right angle. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Pythagorean Theorem says that the sums of the squares of the two shorter sides of a right triangle equals the square of the hypotenuse. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
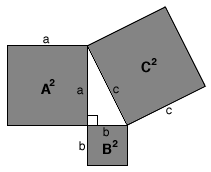
| Take a look at the illustration below. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The formula for the area of a square (of side "a") is written | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| which means a X a or "a times a." It is said out loud as "A SQUARED." | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Pythagorean Theorem can also be written as: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a2 + b2 = c2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Or, as indicated in the shaded squares of the above illustration: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A2 + B2 = C2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| There are many, many ways to prove the theorem. The way shown in The Little Triangle Movie may be the easiest to grasp visually. Use the "Pythagoras Animation" link below to see another animated version of the same proof. This one will show that it will work for right triangles of all shapes and sizes! Use the "Another Pythagoras Animation, Different Proof" link to view a very nice animation that goes about proving the theorem in a different way! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| All of the links below are excellent for fun and learning! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Behold! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussion of the above proof and links. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pythagoras Animation | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Another animation of the proof, very nice and demonstrates for all sizes and shapes of right triangles! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Another Pythagoras Animation, Different Proof | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Nice animation, a different proof, also demonstrates the theorem geometrically! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Cut-the-Knot Site | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Excellent site, very good Pythagoras presentation. Scroll down for links! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| From Pythagoras to Trigonometry | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Excellent interactive site, takes you step-by-step forward from the Pythagorean Theorem. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Historical Background on the Pythagorean Theorem | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Very good description, with picture of statue of Pythagoras (head). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A Pythagorean Theorem Joke | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A joke on the Pythagorean Theorem! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Go to Fred's Main Page or to Fred's Navigator |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Visitors to this page = | since February 19, 1998 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| LinkExchange Member | Free Home Pages at GeoCities | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This page hosted by | Get your own Free Home Page | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||